1.1. Causal Graph
A graph consists of a set of nodes and a set of edges that connect two nodes. Nodes in a graph represent random variables and edges denote relationships among them. Every two nodes are connected by an edge are called adjacent nodes. If every edge in a graph is an arrow pointing from one node to another node, the graph is a directed graph. In such a directed edge, \(X\) is called a parent of \(Y\) and \(Y\) is said to be a child of \(X\). Figure 1 exemplifies some types of graphs.
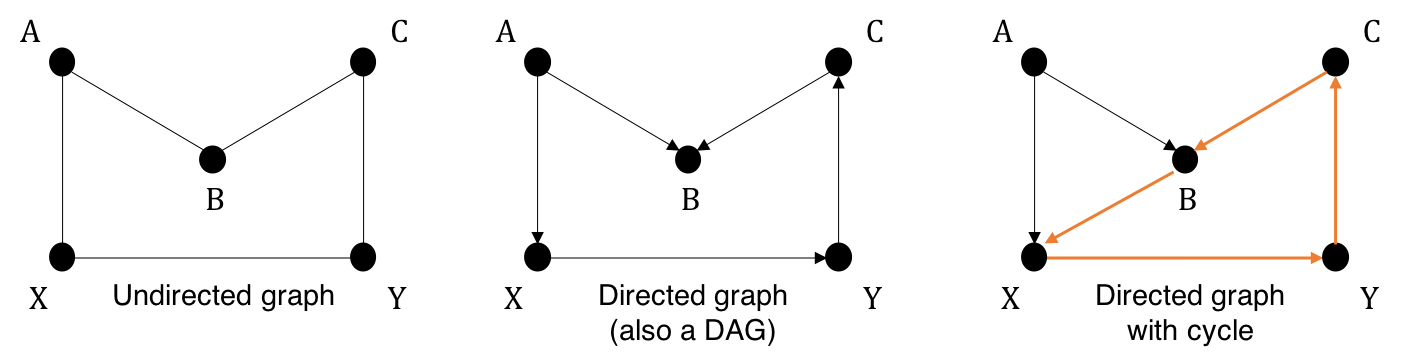
A path in a graph is any sequence of consecutive edges in which the starting node is the ending node of the preceding edge, regardless of their directions. Paths cannot be broken nor intersectting, and if there exists a path between two nodes, they are said to be connected. A directed path is a path that consists of directed edges in the same direction. In a directed path that starts at node \(X\) and ends at node \(Y\), \(X\) is an ancestor of \(Y\), and \(Y\) is a descendant of \(X\). In the middle graph, \(A \rightarrow X \rightarrow Y \rightarrow C \rightarrow B\) is a direct path while \(A \rightarrow X \rightarrow Y \rightarrow C \rightarrow B \leftarrow A\) is not.
A directed path may form a cycle that returns to the starting node. One with no directed cycles is an acyclic graph. We mostly focus on directed acyclic graphs (DAGs).
A causal graph (sometimes called causal diagram) is a graph that models the causal relationships between variables (nodes). Graphical models encode causal relations through
Strict Causal Edges Assumption :
In a directed graph, every parent is a direct cause of all its children.
You may question about the "indirect" cause. Indirect effect is usually discussed in the context of mediation - that is, there exists a path like \(X \rightarrow M \rightarrow Y\) where \(M\) is called a mediator. In such a relationship, \(M\) transmits the causal effect from \(X\) to \(Y\), or we can say that \(X\) indirectly affects \(Y\) through \(M\). This gives rise to several concepts such as Total Effect, Controlled Effect, Natural Direct Effect and Natural Indirect Effect, which will be discussed in Chapter 4.
Generally, when talking about the causal effect of \(X\) on \(Y\), we often mean the direct effect. We then wish to determine whether \(X\) is a parent of \(Y\) and how much \(Y\) changes induced by changes in \(X\).
1.2. Correlation is not Causation
For a causal effect to occur, \(X\) must first be statistically correlated with \(Y\). In other words, if \(X\) causes \(Y\), they are associated, but the fact that they are correlated does not mean there is a true causal effect. This is the fundamental idea behind the adage Correlation is not Causation.
Let's say we have a DAG as in Figure 1.2. There is no direct path between \(X\) and \(Y\), but \(X\) and \(Y\) are correlated because of \(Z\). \(Z\) in such a graph structure is the common cause of \(X\) and \(Y\), which is called a confounder or said to impose a confounding bias. If we only have data on \(X,Y\), we will see that \(X\) varies by different values of \(Y\). This correlation stems from the corresponding variation in \(Z\) to begin with. If we happened to have data on \(Z\), by fixing \(Z\) to a value, it would be observed that no matter how much we change \(X\), \(Y\) would remain unchanged (constant \(Z\) \(\rightarrow\) constant \(Y\)).
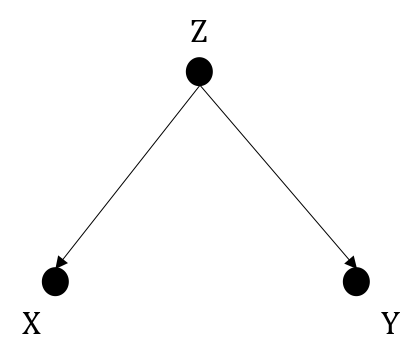
The action of setting a third variable \(Z\) to a fixed value and observe how it impacts the relationship between two other variables is also knowns as adjusting for or controlling for or conditioned on \(Z\). Please note that my conclusion that \(Y\) remains unchanged is based on a critical assumption that \(X\) only connects with \(Y\) through \(Z\). But without data on \(Z\), we would never know. To make it worse, it is also very difficult to tell exactly whether there are any other tricky paths that send a wrong signal.
We are now ready to define everything more rigorously. We quantify causal effects between two random variables using the language of probability. More concretely, researchers leverage methods of probabilistic graphical models to develop theories for Causal Inference. We now take a deeper look into this connection.
1.3. Bayesian Networks
Let's review some basic statistical rules:
- We model the uncertainty of a random variable \(X\) through a probability distribution \(P(X=x),\) measuring the probability of \(X\) taking the value \(x\) (\(0 \le P(X) \le 1\)). It is termed as marginal probability, and \(x\) is called a realization of \(X\). \(X\) can be discreet, continuous, or multi-dimensional.
- Two random variables \(X\) and \(Y\) are said to be independent, denoted as \(X \perp\!\!\!\!\perp Y\), if the occurence of \(X\) does not affect the probability of \(Y\) occuring. Mathematically, $$X \perp\!\!\!\!\perp Y \Leftrightarrow P(X,Y) = P(X)P(Y)$$ where \(P(X,Y)\) is the joint distribution. \(P(X=x,Y=y)\) is the probability of observing \(X=x\) and \(Y=y\) at the same time.
- \(P(X|Y)\) or specifically \(P(X=x|Y=y)\) measures the probabilty \(X=x\) if we observe \(Y=y.\) This is termed as conditional probability. It basically says how much the knowledge about \(X\) to be updated given additional information about \(Y\). If \(X\) and \(Y\) are independent, \(P(X|Y)=Y\). Knowing \(Y\) gives no information about \(X\).
- By Sum and Product rule, $$\sum_aP(A) = 1 \quad \text{where } a \text{ are all realizations of } A$$ $$P(A) = \sum_bP(A,B) \quad \text{where } b \text{ are all realizations of } B$$ $$P(A|B) = \frac{P(A,B)}{P(B)} $$
Bayesian Network Factorization :
Given a probability distribution \(P\) and a DAG \(G\), the joint distribution of \(n\) nodes in \(G\) is given as $$P(X_1, X_2, ..., X_n) = \prod_i P(X_i|PA_i)$$ with \(PA_i\) being all parents of node \(X_i\).
Expressed in words,
Minimality Assumption :
- A node \(X\) is independent of all its non-descendants conditioned on its parents in a DAG
(Local Markov Assumption) - Adjacent nodes in the DAG are dependent.
The joint distribtuion in Figure 1.2 can be factorized into $$P(X,Y,Z) = P(X|Z)P(Y|Z)P(Z)$$ Again, this is done by multiplying independent terms together.
1.4. Graph Building Blocks
A path between two nodes \(X\) and \(Y\) is blocked by a node \(Z\) if \(X \perp\!\!\!\!\perp Y | Z\). Controlling for \(Z\) stops information from flowing between them, thereby eliminating the association. Interestingly, causal DAGs offer a quick test of independence among nodes, powered by \(d-\)Separation criterion.
Definition of \(d-\)Separation :
A path \(p\) between two nodes \(i,j\) is said to be \(d-\)separated by a set of nodes in \(Z\) if and only if
- \(p\) contains a chain \(i \rightarrow m \rightarrow j\) or a fork \(i \leftarrow m \rightarrow j\) such that \(m\) in \(Z\)
- \(p\) contains a collider \(i \rightarrow m \leftarrow j\) such that \(m\) not in \(Z\) and no descendants of \(m\) is in \(Z\)
The condition that translates conditional independence into \(d-\)separation is Markov Compatibility.
Markov Compatibility :
If a (joint) probability function \(P\) admits the factorization of Bayesian Network relative to a DAG \(G\), we say that \(G\) represents \(P\), that \(G\) and \(P\) are compatible or \(P\) is Markov relative to \(G\).
Figure 1.2 is an example of a fork. Here is a proof why \(d-\)separation is valid. We need to prove given such a DAG, \(X\) is independent of \(Y\) given \(Z\), or \(X \perp\!\!\!\!\perp Y|Z\) $$P(X,Y,Z) = P(X|Z)P(Y|Z)P(Z) \Leftrightarrow \frac{P(X,Y,Z)}{P(Z)} = P(X|Z)P(Y|Z)$$ $$\Leftrightarrow P(X,Y|Z) = P(X|Z)P(Y|Z)$$
Proving \(d-\)separation for a chain is also trivial. I leave it as a small exercise for you.
We will quickly prove the case where \(Z\) is collider. Consider Figure 1.3,
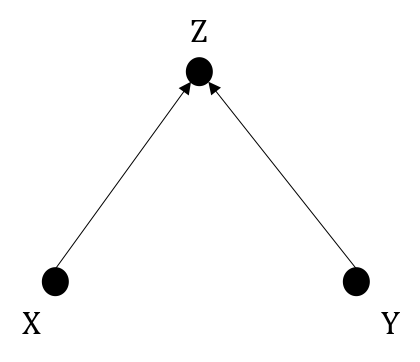
We can easily prove that \(X\) and \(Y\) are marginally independent in such a graph. $$P(X,Y)=\sum_zP(X,Y,Z)=\sum_zP(X)P(Y)P(Z|X,Y)=P(X)P(Y)\sum_zP(Z|X,Y)$$ By summing all realizations of \(Z\), we have \(\sum_zP(Z|X,Y)=1\), yielding \(P(X,Y)=P(X)P(Y)\).
If \(X,Y\) are marginally independent, conditioning \(X,Y\) on the collider opens the association flow between \(X\) and \(Y\). We need to prove \(X|Z\) and \(Y|Z\) are dependent.
\(X,Y\) are common causes of \(Z\). \(P(X|Z)\) and \(P(Y|Z)\) are concerned when we wish to infer the cause from effect. The intuition is that the information on whether a cause occurs influences the belief in the occurence of the other cause. Let's say you have a headache, and suppose it is either because you have a brain tumor or due to lack of sleep. Finding yourself suffering poor sleep for the past days increases the chance of sleep deprivation being the cause, thus reducing the probability of having brain tumor.
What we have discussed so far is summarized into Global Markov Assumption.
Global Markov Assumption :
Given that \(P\) and \(G\) are compatible, if \(X\) and \(Y\) are \(d-\)separated in \(G\) conditioned on \(Z\), \(X\) and \(Y\) are independent conditioned on \(Z\). Mathematically, $$X \perp\!\!\!\!\perp_G Y|Z \Rightarrow X \perp\!\!\!\!\perp_P Y|Z$$
Note that the other direction may not be true.
1.5. Assocation vs. Intervention
Pearl clarifies the discrepancy between Correlation and Causation through the concepts of Interventional distribution, denoted as \(P(Y|do(X))\). This is fundamentally different from Observational distribution \(P(Y|X)\) in our discussion so far. Take a population of interest,
- \(P(Y|X=x)\) gives information about \(Y\) within the subset of population with value \(X=x\).
- \(P(Y|do(X=x))\) tells us what happens to \(Y\) when we force all observations in the population to have \(X=x\).
The term Intervention is used in an active sense that refers to imposing a certain action on variable \(X\). We often examine hard intervention in which \(X\) is set to a constant value \(x\), that is \(do(X=x)\). Notice the difference: \(X\) is random variable that can take a realization \(x\), \(do(X=x)\) is a distribution that is fixed to value \(x\).
Intervention is critical to establishing causal relations. By intervening on \(X\), we eliminate all confounding biases that may intercept the relationship between \(X\) and \(Y\). After the intervention, any effects on \(Y\) related to \(X\) are considered the causal effects of \(X\) on \(Y\). We will see how and why this is the case more practically when discussing Potential Outcome in Part II: Experimentation.
It turns out that graphical models can be used to model Interventional distribution. A causal graph for interventional distribution is constructed by deleting all the edges to the intervened nodes in the graph for observational distribution. Because \(X\) is now fixed, it no longer depends on any its original parents. In other words, intervened nodes have no causal parents. We call this the manipulated graph. A mathematical equivalence of this concept will be provided in section 2.4.
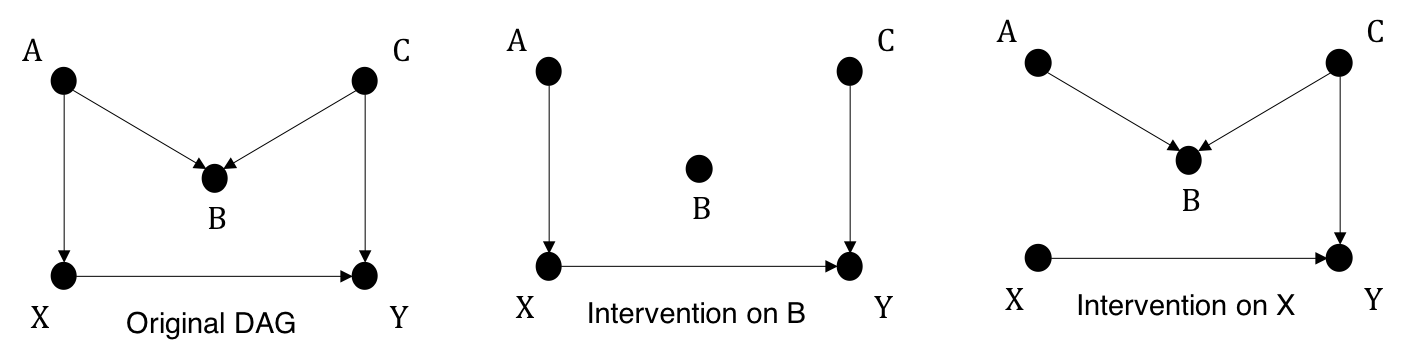
All directed paths pointing into a node \(X_i\) in a DAG \(G\) form the causal mechanism or causal generative process of \(X_i\) with respect to \(G\), modelled as \(P(X_i|PA_i)\). Unless we have data on all possible parents of \(X_i\) in reality, the true data generating process for \(X_i\) always remains unknown.
One important property is that intervening on a node \(X_i\) does not alter the causal mechanisms of other nodes. The conditional distribution of each variable given its causes (i.e., its mechanism) does not inform or influence the other conditional distributions. Interventions are thus localized, and causal mechanisms are autonomous, modular or invariant. This is Reichenbach's Principles of Independent Mechanisms. We have the following assumption:
Modularity Assumption ~ Causal Bayesian Network :
If we perform hard intervention on a subset of nodes \(S\) in a set of \(n\) nodes \(X\) by setting them to constant \(x\), \(\forall i\)
- If node \(X_i \notin S\), \(P(X_i|PA_i)\) remains unchanged
- If node \(X_i \in S\), \(P(X_i|PA_i)=1\) if \(X_i\) is set to \(x\) or \(do(X_i=x)\); otherwise \(P(X_i|PA_i)=0\)
We can now compute the interventional distribution by using Truncated Factorization.
Truncated Factorization :
Given \(P\) and compatible DAG \(G\), let's denote the interventional distribution of \(n\) nodes in \(G\) when intervening on a set of nodes \(S\) to by fixing them on a constant \(x\), \(P(X_1, ..., X_n|do(S=x))\).
If every node in \(S\) is truly set to \(x\), or \(x\) is consistent with the intervention $$P(X_1, ..., X_n|do(S=x)) = \prod_{i \notin S}P(X_i|PA_i)$$
If every node in \(S\) is truly set to any other value \(x' \ne x\), or \(x\) is inconsistent with the intervention $$P(X_1, ..., X_n|do(S=x))=0$$
1.6. Identifiability
In summary, \(P(Y|do(X))\) is a causal estimand that estimates the causal effect of \(X\) on \(Y\) while \(P(Y|X)\) is a statistical estimand that simply tells us how much \(Y\) varies by different values of \(X\), without making any causal claims. Interventions by our definition are unrealistic and in practice equivalent to conducting experiments. The question is, based on all the tools we have, can we identify the causal effects between \(X\) and \(Y\)?
The answer is, given \(P, G\) along with all constraints above satisfied, under certain conditions, we can transform causal estimands into statistical estimands that can be computed directly from observational data without doing experiments (the term non-experimental data is often used interchangeably).
If we can reduce an expression with the \(do\) operator in it to one without do, then the causal effect is said to be identifiable. \(Do-\)Calculus is a general framework to identify causal effects. We define it formally here
Causal Effect Identifiability :
A causal effect \(q=P(Y_1,...,Y_k|do(X_1),...do(X_s))\) is identifiable in a model characterized by a graph \(G\) if there exists a sequence of finite transformations, each conforming to one of the inference rules in \(Do-\)Calculus, that reduces \(q\) into a standard probability expression involved observed quantities.
The next chapter details what is \(Do-\)Calculus and how to determine causal effects.
