Assume we are given an observational dataset of \(V\) observed variables and causal graph \(G\). The set \(V\) includes a treatment variable \(X\) and a outcome variable \(Y\) of interest, and we wish to determine the effect on \(Y\) under the intervention \(do(X=x)\) – that is, to estimate the interventional distribution \(P(y|do(x)\)).
Recall that \(X\) and \(Y\) are not neccessarily single variables, rather each of them can be a subset of \(n\) variables in \(V\) and mathematically represented as an \(n\)-dimensional vector. Identification methods can be broadly categorized as Non-parametric or Parametric.
We first go through the theoretical concepts in this chapter and continue to deepen our understanding through a case study in the Chapter 3.
Table of Contents
Non-parametric methods
Parametric methods
Under certain conditions, these methods allow us to estimate \(P(y|do(x))\) (i.e., a causal estimand) from statistical quantities to be computed directly from the data. The idea is to pass the causal estimand through a series of transformations that output an equivalent combination of statistical estimands, which must be derived from plausible probability rules based on the assumptions and properties we have discussed so far.
2.1. Back-Door Criterion
Back-Door Criterion Definition :
A set of variables \(Z\) in \(V\) satisfies the back-door criterion relative to \(X\) and \(Y\) in a DAG \(G\) if- no node in \(Z\) is a descendent of \(X\)
- \(Z\) blocks every path between \(X\) and \(Y\) that contains an arrow into \(X\)
This definition is followed by
Back-Door Adjustment Theorem :
If \(Z\) satisfies the back-door criterion relative to (\(X,Y\)), the causal effect of \(X\) on \(Y\) is identified as $$P(y|do(x)) = \sum_{z}P(y|x,z)P(z)$$The theorem aligns with our intuition above: If \(Z\) blocks all back-door paths between \(X\) and \(Y\), there will be no confounding biases, thus rendering any associational effects be the true causal effect. We will add a causal link \(X \rightarrow Y\) in Figure 1.2, which gives a simple example where \(Z\) is a back-door criterion (right). And when doing intervention, we estimated the effect based on the manipulated graph (right), in which the incoming edge into \(X\) from \(Z\) is removed. I provide a step-by-step proof to solidify the intuition.
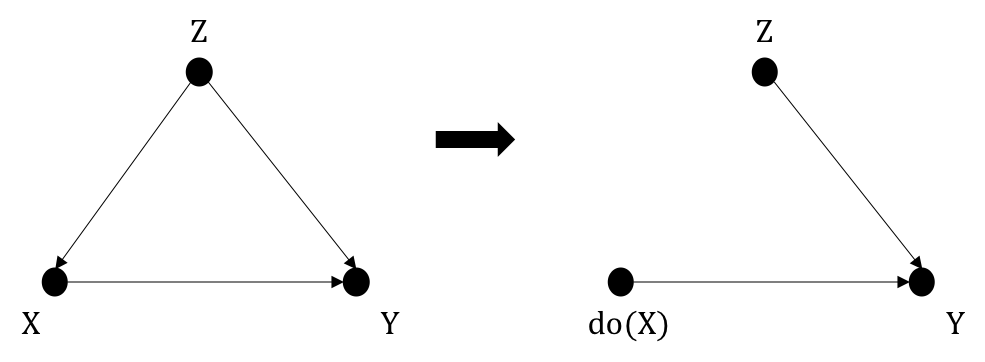
- By probability rules, $$P(y|do(x)) = \frac{P(y,do(x))}{P(do(x))} = \frac{\sum_{z}P(y,do(x),z)}{P(do(x))} = \frac{\sum_{z}P(y|do(x),z)P(do(x),z)}{P(do(x))}$$ $$= \frac{\sum_{z}P(y|do(x),z)P(z|do(x))P(do(x))}{P(do(x))} = \sum_{z}P(y|do(x),z)P(z|do(x))) $$
- By Modularity assumption, \(Y\) is not the intervention node so \(P(y|pa_y)\) under the intervention remains unchanged. This yields \(P(y|do(x),z) = P(y|x, z)\). This equality holds even when \(Z\) is not the parent of \(Y\) but still satisfies the back-door criterion.
- Assume there are no other back-door paths \(X-Z\), \(Z\) does not depend on \(X\), so \(P(z|do(x))=P(z)\). This is justified by observing that \(Z\) is independent of \(do(x)\) in the manipulated graph, but not independent of \(X\). Notice that you could also have directly derived \(P(do(x),z) = P(do(x))P(z)\) due to this non-dependency.
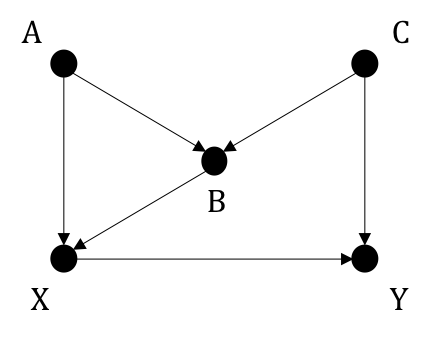
There are two paths with arrows pointing into \(X\): \(X \leftarrow A \rightarrow B \leftarrow C \rightarrow Y\) and \(X \leftarrow B \leftarrow C \rightarrow Y\). If we condition on \(B\) to block the second path, it opens up the first back-door path since \(B\) is a collider. We therefore must further control for \(A,C\). However, we can also only control for \(C\) to block the second path while the leaving the first path already been blocked by \(B\). Thus, the back-door criterion is either \(C\) or the set {\(A,B,C\)}.
2.2. Front-Door Criterion
Assume we have a graph \(G\) as follow, where the confounder \(Z\) is unobserved. Thus, blocking the back-door
is impossible.
Fortunately, we can take advantage of such a variable as \(M\) - a mediator such that all causal paths from
\(X\) to \(Y\) must go through \(M\).
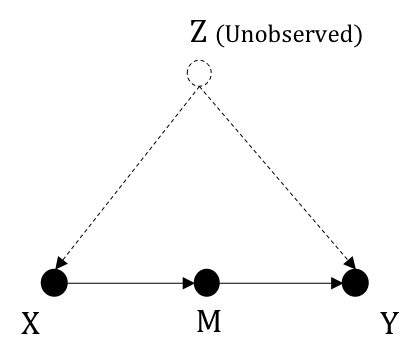
Front-Door Criterion Definition :
A set of variables \(M\) satisfies the front-door criterion relative to \(X, Y\) and \(Y\) if- \(M\) mediates all directed paths from \(X\) to \(Y\)
- there is no unblocked back-door path from \(X\) to \(M\)
- all back-door paths from \(M\) to \(Y\) are blocked by \(X\)
This definition is followed by
Front-Door Adjustment Theorem :
If \(M\) satisfies the front-door criterion relative to (\(X,Y\)) and \(P(x, m) > 0\), the causal effect of \(X\) on \(Y\) is identified as $$P(y|do(x)) = \sum_{m}P(m|x)\sum_{x'}P(y|x',m)P(x')$$With \(M\) being a front-door criterion, the causal effect can be determined through the following steps (Pearl 2009; Neal 2020)
Step 1: Identify the causal effect of \(X\) on \(M\)
Notice that \(Y\) is a collider blocking the back-door path \(X \leftarrow Z \rightarrow Y \leftarrow M\). \(X \rightarrow M\) is the direct causal path. $$P(m|do(x) = P(m|x))$$
Step 2: Identify the causal effect of \(M\) on \(Y\)
The back-door path \(M \leftarrow X \leftarrow Z \rightarrow Y\) can be blocked by conditioning on \(X\). In other words, we can use Back-door Adjustment on \(X\). $$P(y|do(m)) = \sum_{x'}P(y|m, x')P(x'))$$ We use \(x'\) to distinguish this random value with the interventional value \(X=x\)
Step 3: Combine the two effects to identify the causal effect of \(X\) on \(Y\)
By first setting \(X=x\), we observe the value \(M=m\). We then set \(M\) to this value \(m\) and evaluate \(Y\). If \(M=m\) every time we set \(X\) to \(x\), the combined effect would be exactly \(P(y|do(m)\). In fact, \(M\) returns multiple values \(m\) corresponding to \(X=x\) with probability \(P(m|do(x))\). Thus, the combined effect is generally calculated by summing the effects on \(Y\) observed when \(M=m\) weighted by the probablity that value \(m\) occurs. $$P(y|do(x)) = \sum_{m}P(m|do(x)P(y|do(m))$$ Substituting the results from step (1) and (2) yield the theorem, in which all quantities can be estimated.
2.3. \(Do\) Calculus
\(Do\) calculus is a set of general inference rules that are proved to be sufficient to identify all causal estimands given that they are identifiable. These rules not only generalize the Back-door criterion and Front-door criterion, but is also valid when neither criteria is satisfied. I attempt to introduce the rules and convey the intuition to aid your understanding. Rigorous explanation can be found in Causal diagrams for empirical research (Pearl 1995, p.687).
Given a DAG \(G\), we denote \(G_{\bar{X}}\) the graph obtained by deleting from \(G\) all incoming edges to nodes in \(X\). We denote \(G_{\underline{X}}\) the graph obtained by deleting from \(G\) all outgoing edges from nodes in \(X\). To make it general, we begin with the interventional distribution \(P(y|do(x))\), induced by the intervention \(do(X) = x\) We therefore have the manipulated graph \(G_{\bar{X}}\) as the base graph. You can safely ignore the term \(do(X)\) to better understand these expressions, For any disjoint subsets of variables \(X,Y,Z,W\), we have the following rules
\(Do\)-calculus Theorem
Rule 1: Insertion/Deletion of observations
$$P(y|do(x),z,w) = P(y|do(x),w) \quad if \quad (Y \perp\!\!\!\!\perp Z)|X,W \quad w.r.t \quad G_{\bar{X}}$$Rule 1 confirms \(d\)-separation. The condition simply means adjusting {\(X,W\)} blocks all possible back-door paths from \(Z\) to \(Y\). When found independent with \(Y\), \(Z\) become irrelevant, thus can be removed or included freely.
\(Do\)-calculus Theorem
Rule 2: Action/Observation change
$$P(y|do(x),do(z),w) = P(y|do(x),z,w) \quad if \quad (Y \perp\!\!\!\!\perp Z)|X,W \quad w.r.t \quad G_{\bar{X}\underline{Z}}$$Examining the effect of action \(do(Z) = z\) on \(Y\) implies the original graph contains a path with an arrow outgoing from \(Z\) pointing into \(Y\). If we disconnect the causal path from \(Z\) to \(Y\), thereby ending up with \(G_{\underline{Z}}\) and observe that all back-door paths are blocked by {\(X,W\)}, the association flow between \(Z\) and \(Y\) is the causal flow. Setting \(Z=z\) or conditioning on \(Z=z\) yields the same effect. In other words, correlation is now causation.
\(Do\)-calculus Theorem
Rule 3: Insertion/Deletion of actions
$$P(y|do(x),do(z),w) = P(y|do(x),w) \quad if \quad (Y \perp\!\!\!\!\perp Z)|X,W \quad w.r.t \quad G_{\overline{XZ(W)}}$$ where \(Z(W)\) is the set of \(Z\)-nodes that are not ancestors of any \(W\)-node in \(G_{\bar{X}}\)
Let \(\widetilde{Z(W)}\) denote the set of \(Z\)-nodes that are the ancestors of \(W\).
Hence, we end up with the (indirect) causal path from \(\widetilde{Z(W)}\) to \(W\) as below, whereas
because no nodes in \(Z(W)\) are ancestors of \(W\), at least one node in \(Z(W)\) is a descendent of
nodes in \(\widetilde{Z(W)}\) (DAG cannot be disconnected). Furthermore, it is either that \(Z(W)\)
and \(W\) are not linked or nodes in \(Z(W)\) are descendents of \(W\).
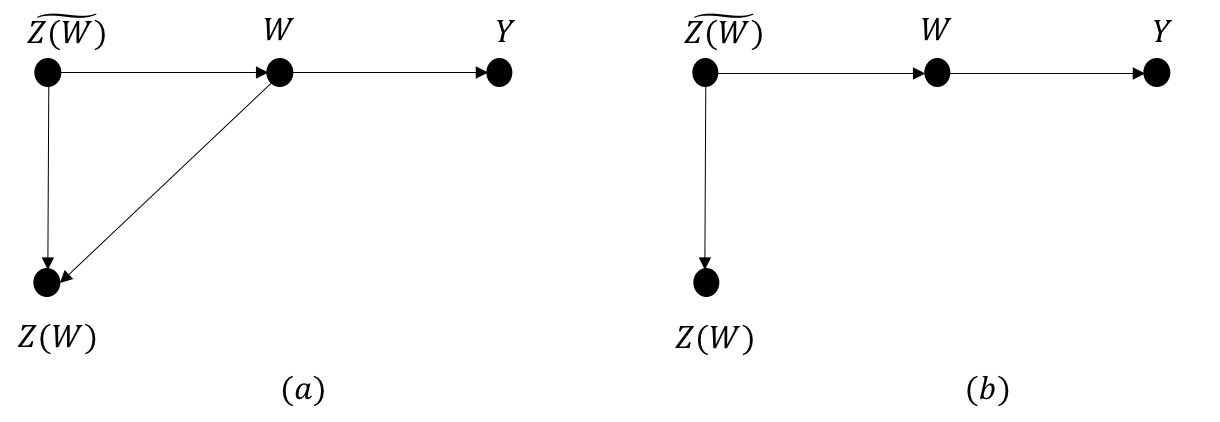
Recall that we are still working on the manipulated graph \(G_{\bar{X}}\). Safely ignoring \(X\), for \(Y\) to be independent on \(Z\) given \(W\), \(W\) must both block all paths between \(\widetilde{Z(W)}\) and \(Y\) and all paths between \(Z(W)\) and \(Y\). Thus, the path from \(Z\) to \(Y\) must go through \(W\). The graph \(G_{\overline{Z(W)}}\) is constructed by removing all incoming edges to \(Z(W)\). The conditional independency ensures the only back-door path between \(Z\) and \(Y\) is one going through \(W\). Other than that, there is no unblocked path. Returning to the original graph \(G_{\bar{X}}\), \(d\)-separation tells us that conditionining on \(W\) prevents information flowing from \(Z\) to \(Y\). As a result, any action taken on \(Z\) would have no effect on \(Y\).
2.4. Structural Causal Models
Instrumental variables is called parametric methods because they require parametric modelling of causal mechanisms - in a simpler sense, a mathematical function encoding causal relationships. Indeed, so far we have only discussed, through graphical models, how to disconnect spurious associational path in order to unveil genuine causal effects, but yet to explain exactly how to quantify the magnitude. Structural equations provide mathematical tools to do this.
2.4.1. Redefine Causal Mechanism
We can represent the statement \(X\) is a cause of \(Y\) mathematically through some function \(f\) that maps \(X\) to \(Y\). More generally, a structural equation representing a variable is a functional form of all its parent variables. In practice, we hardly know all possible direct causes of a variable, so we factor in this stochastic nature by adding some unobserved noise random variable \(U\). $$Y := f_Y(X, U)$$
Notice that \(:=\) is used instead of the equal sign \(=\), which says \(f_Y\) is the causal generative distribution of \(Y\). The purpose is again, to distinguish statistical modelling of \(Y\) from \(X\) (e.g.,a regression model) that uses the equal sign. This leads to more concrete definitions of a cause and a causal mechanism.
Definition of Cause and Causal Mechanism :
A causal mechanism that generates a variable \(V\) is the structural equation that corresponds to that variable. Other variables that appear on the right-hand side of that structural equation are direct causes of \(V\).
We model the causal mechanism of a system (1) graphically via a causal graph and (2) mathematically through a structural causal model (SCM).
Definition of Structural Causal Model :
A structural causal model is a tuple of the following sets:
- A set of endogenous variables \(V\)
- A set of exogenous variables \(U\)
- A set of functions \(f\), one to generate each endogenous variable as a function of other variables.
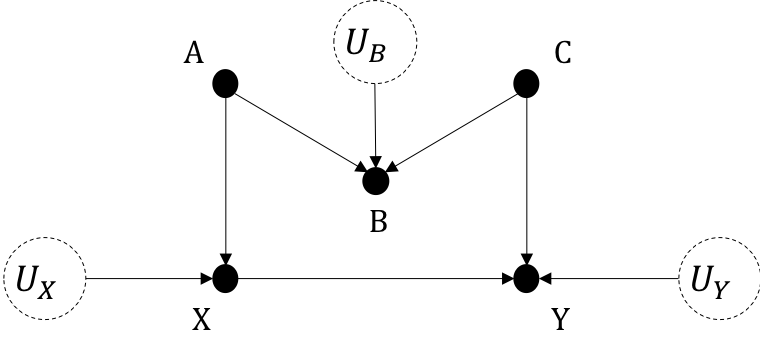
Exogenous variables are ones without any parents in the causal graph, external to the system. Endogenous variables have parents and are those we model. The SCM for the causal graph in Figure 2.4 is written as $$X:=f_X(A,U_X)$$ $$B:=f_B(A,C,U_B)$$ $$Y:=f_Y(X,C,U_Y)$$ where {\(X,B,Y\)} are endogenous and {\(A,C,U_X,U_B,U_Y\)} are exogenous.
2.4.2. Intervention in SCM
If regarded as a causal model, then SCM must also be used to model interventional distribution. Intervention \(do(X)=x\) is equivalent to setting the structual equation of \(X\) to \(x\). Let's review the manipulated graphs in Figure 1.4
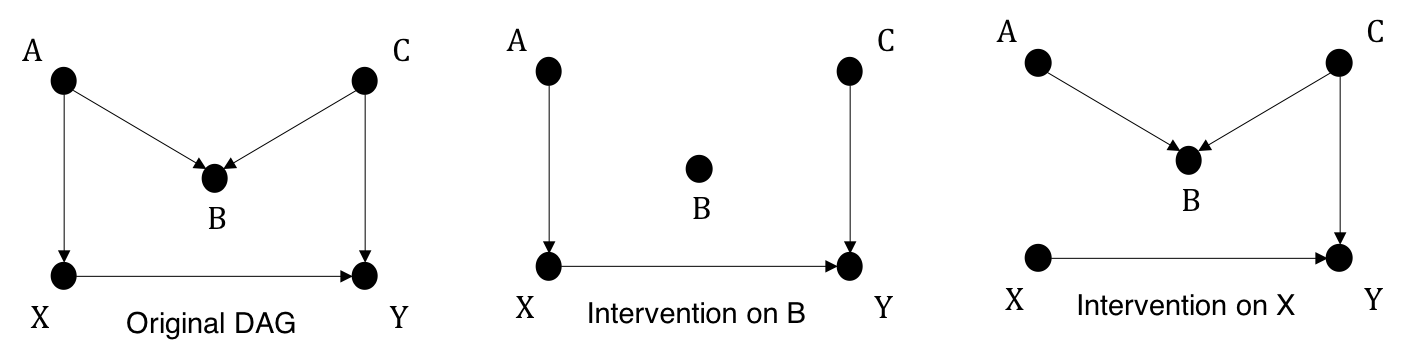
The interventional SCM upon intervention on \(X\), with respect to the third graph is $$X:=x$$ $$B:=f_B(A,C,U_B)$$ $$Y:=f_Y(X=x,C,U_Y)$$
This strongly aligns with our definition of interventional distribution in Chapter 1. Fixing \(X\) to a constant distribution completely eliminates the dependence between \(X\) and its parents, which is equivalent to deleting any arrows pointing into \(X\) in the graph. In addition, setting \(X\) to a constant \(x\) is called hard intervention. Under SCM, you can see that we can be more flexible by assigning \(X\) to a new distribution i.e., new causal mechanism to \(X\). Such action is referred to as soft intervention.
2.5. Average Causal Effect
A quick review of expected value:
The expected value of a random variable \(X\), denoted as \(E[X]\), is the generalization of weighted
average given as
$$E[X] = \int xP(x) dx$$
If \(X\) is a discreet variable with finite outcomes \(x_1, x_2, ..., x_n\) occuring with probabilities \(P_1,
P_2, ..., P_n\),
$$E[X] = \sum_{i=1}^{n} x_i P_i$$
Linearity of Expectation:
$$E[X+Y] = E[X]+E[Y]$$
If \(X\) and \(Y\) are independent,
$$E[XY] = E[X]E[Y]$$
Until this point, we have only discussed \(P(Y|do(X))\) as the interventional distribution of \(Y\) - that is, possible values \(Y\) can attain, along with the probabilities of occurence when \(X\) is forced to take a certain value.
Now there comes an official definition of causal effects. When \(X\) changes from \(x_1\) to \(x_2\), for an individual \(i\) in the population, the individual causal effect on \(Y\) is defined as $$Y_i|do(X=x_2) - Y_i|do(X=x_1)$$ As we wish to estimate causal effect on the population level, we choose to measure the average causal effect, given as $$E[Y|do(X=x_2)] - E[Y|do(X=x_1)] $$ If the above quantity is zero, we say such a change in \(X\) has no causal effect on \(Y\).
2.6. Instrumental Variables
The method of Instrumental variables allows for identification where there is unobserved confounding or absence of mediator.
Definition of Instrumental variable :
\(Z\) is considered an instrument if satisfying the following assumptions- \(Z\) has a causal effect on \(X\).
- \(X\) is a mediator on the causal path from \(Z\) to \(Y\).
- There are no backdoor paths from \(Z\) to \(Y\).
Figure 2.5 illustrates a causal graph where \(Z\) is an observed instrumental variable while the confounder \(U\) is not observed.
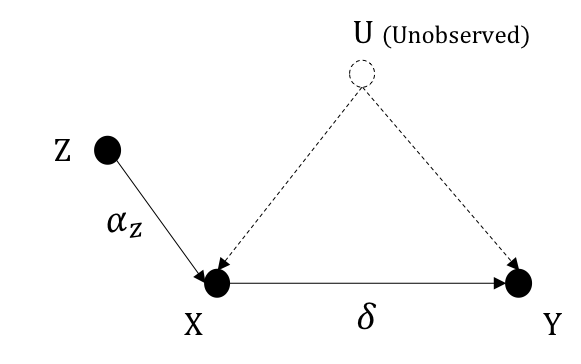
We assume the SCM takes a linear form defined as $$X:= \alpha_z Z$$ $$Y := \delta X + \alpha_uU$$ where \(\delta\), structural coefficients, measures how much \(Y\) varies caused by \(1\) unit change in \(X\). Based on the specified model, \(\delta\) measures the causal effect between \(X\) and \(Y\) – the causal quantity to be estimated. The following section shows how to derive \(\delta\) from statistical quantities.
When \(X,Z\) is binary:$$E[Y|Z=1] - E[Y|Z=0] = E[\delta X + \alpha_u U|Z=1] - E[\delta X + \alpha_u U|Z=0]$$ ≫ Rearranging using properties of expectation: $$E[Y|Z=1] - E[Y|Z=0] = \delta (E[X|Z=1] - E[X|Z=0]) + \alpha_U (E[U|Z=1] - E[U|Z=0])$$
Because there is no back-door path between \(Z\) and \(U\) and the graph says \(Z \perp\!\!\!\!\perp U\) due to the collider \(X\), the second term in the right-hand side is zero. We therefore have $$\delta = \frac{E[Y|Z=1] - E[Y|Z=0]}{E[X|Z=1] - E[X|Z=0]} $$
Here \(Z\) is assumed to have causal effect on \(X\), so regardless of any back-door paths or any potential mediators between them, \(\alpha_z\) measures the causal effect between \(Z\) and \(X\), and $$\alpha_z = E[X|Z=1] - E[X|Z=0]$$ So, in linear settings, the total effect of \(Z\) on \(Y\) is $$E[Y|Z=1] - E[Y|Z=0] = \alpha_U \delta$$
When \(X,Z\) is continuous:Similarly, we begin with the observational covariance between \(Y\) and \(Z\) – \(\text{Cov}(Y,Z)\). Its formula is given in the first line. $$\text{Cov}(Y,Z) = E[YZ] - E[Y]E[Z]$$ ≫ Injecting structural equation for \(Y\): $$\text{Cov}(Y,Z) = E[(\delta X + \alpha_uU)Z] - E[Y]E[Z]$$ ≫ Rearranging using properties of expectation: $$\text{Cov}(Y,Z) = \delta (E[XZ]-E[X]E[Z]) + \alpha_u (E[UZ]-E[U]E[Z]) = \delta \text{Cov}(X,Z) + \alpha_u \text{Cov}(U,Z) $$
\(\text{Cov}(U,Z) = 0\) because \(Z \perp\!\!\!\!\perp U\). We thus settle with the causal effect identified as $$\delta = \frac{\text{Cov}(Y,Z)}{\text{Cov}(X,Z)}$$
Instrumental variables are not restricted to linear equations. We can apply the same idea on any functional forms compatible with the causal mechanism. The first important step is to detect an instrumental candidate and use non-parametric methods to block the back-door paths from that variable to outcome variable \(Y\). Once all the conditions met, we can develop a series of manipulations to convert \(\delta\) to combinations of measurable quantities. With the properly constructed causal graph and SCM, estimation is no longer challenging due to the capacity of neural networks to well enough approximate any relationships in the data.
