Causal Data Science: A Beginner Guide

4.1. Counterfactuals

Suppose you have a headache, you are made to take a pill and observe that the headache goes away. This is, again, an example of intervention and its outcome is the causal effect of the pill on your headache. A counterfactual query is that given the fact that you are cured of the headache, would it still disappear had you not taken the pill? Doing this requires us to imagine what would happen if something did not happen in real world had happened in the past, that is to engage in a counterfactual world. Answering such a question is not always feasible since you cannot redo the experiment. Fortunately, under certain conditions, we can estimate counterfactual effects through observational and interventional data.

The following discusses steps to determine counterfactual quantities at the unit or individual level. This requires a parametric form for our SCM. Let's examine this example.

Let \(Q\) be the quantity of products sold, \(P\) be price per unit of your company and \(C\) be price per unit of your competitor. The SCM is given as $$Q = 2C - P + U_Q$$ $$P = 0.8C+ U_P$$ \(U_Q, U_P\) are repsectively unobserved additive noise variables.

Last year, your product was priced at \(P = \$2\), the competitor's product was priced at \(C = \$3\) and \(10\) units was sold.

Step 1 (Abduction): Use the factual evidence to estimate the exogenous variables \(U_Q\) and \(U_P\). $$ U_Q = Q - 2C + P = 10 - 2 \times 3 + 2 = 6$$ $$ U_P = P - 0.8C = 2 - 0.8 \times 3 = - 0.4$$

Step 2 (Action): Use the \(do-\)operator to change the model to reflect the counterfactual assumption being made. Conducting the intervention \(do(P) = 1\) results in the manipulated SCM $$Q = 2C - 1 + U_Q$$ $$P = 1$$

Step 3 (Prediction): Use the modified model and updated information about the unobserved factors to calculate the counterfactual effects $$Q_{P=2, Q=3}(P=1) = 2 \times 3 - 1 + 6 = 11$$ The notation \(Q_{P=2, Q=3}(P=1)\) indicates the counterfactual quantity is quantified given the known reality of \(P=2, Q=3\). This quantity is fundamentally different from \(Q(P=1)\), which in this case measures the causal effect of changing the price.

Step 1 (Abduction): Same as above

Step 2 (Action): The modified SCM with respect to the intervention \(do(Q) = 1\) is $$Q = 2 \times 1 - P + U_Q$$ $$P = 0.8 \times 1 + U_P$$

Step 3 (Prediction): Because \(C\) influences \(P\), we must first factor in the resulting change in \(P\) at the new level of \(C\) $$P = 0.8 \times 1 - 0.4 = 0.4$$ The counterfactual effect is $$Q_{P=2, Q=3}(Q=1) = 2 \times 1 - 0.4 + 6 = 7.6$$

Your sales would have been reduced had the competitor lowered their price. In question 2, you allow your product's price to respond to the changes in the competitor's price. Alternatively, you may be interested in what the effect would be had the competitor reduced the price while your priced remained fixed. The intervention would now be \(\{do(Q) = 1, do(P) = 2\}\). The counterfactual effect becomes $$Q_{P=2, Q=3}(Q=1, P=2) = 2 \times 1 - 2 + 6 = 6$$ This means you would have to lower your price accordingly to remain competitive.

Here we only examine the simplest case wherein our structural equations are deterministic. A more complicated case is when the exogenous variables vary stochastically or even when the functions \(Q, P\) is not invertible to compute \(U\) values. Stochastic and population-level counterfactual inference are beyond the scope of this book. Advanced readers are encouraged to visit Causality (Pearl 2009) and Identifiability of Path-Specific Effects (Avin et al. 2005).

We now move on to Mediation Analysis - one important application of Counterfactuals.

4.2. Mediation Analysis

In section 1.1, we briefly mentioned \(M\) as a mediator in the causal path from \(X\) to \(Y\). Until this point, we have seen two cases of using mediators: a mediator can be used as a front-door criterion to estimate causal effects in the presence of possible unobserved confounders, or the effect of a mediator on the outcome variable can be identified from instrumental variables.

The setting of Mediation Analysis given in Figure 4.1, where the effect of \(X\) on \(Y\) goes through two paths: the direct path \(X \rightarrow Y\) and the indirect path transmitted through \(X \rightarrow M \rightarrow Y\). The unobserved factors may or may not be correlated with one another.

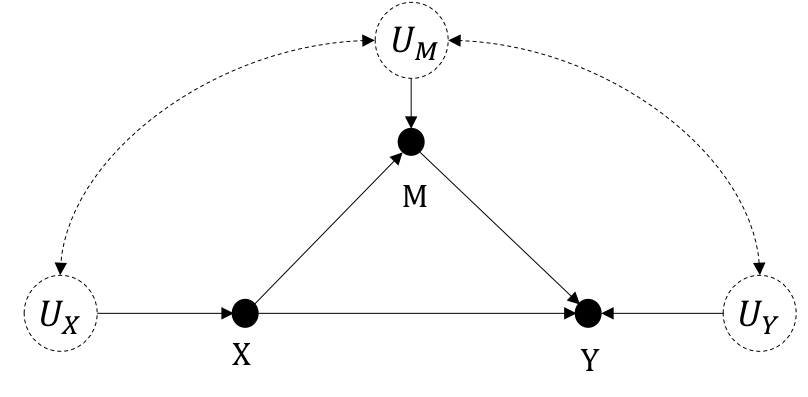
The SCM for such a graph is $$M = f_M(X, U_M)$$ $$X = f_X(U_X)$$ $$Y = f_Y(X, M, U_Y)$$

The effect of \(X\) on \(Y\) is broken into:

1. Total Effect:

   $$TE = E[f_Y(x_2, f_M(x_2, U_M), U_Y)] - E[f_Y(x_1, f_M(x_1, U_M), U_Y)]$$ $$TE = E[Y|do(X=x_2)] - E[Y|do(X=x_1)]$$

   \(TE\) measures the expected change in the outcome \(Y\) when \(X\) changes from \(X=x_1\) to \(X=x_2\). The total effect already incorporates changes in \(M\) induced by intervention on \(X\).

2. Controlled Direct Effect:

   $$CDE(m) = E[f_Y(x_2, f_M(m, U_M), U_Y)] - E[f_Y(x_1, f_M(m, U_M), U_Y)]$$ $$CDE(m) = E[Y|do(X=x_2, M=m)] - E[Y|do(X=x_1, M=m)]$$

   \(CDE\) measures the expected change in the outcome \(Y\) when \(X\) changes \(X=x_1\) to \(X=x_2\), and \(M\) is set to a pre-specified level \(M=m\) over the entire population. It is called controlled direct effect because we control for the effect of the mediator, by interventioning on \(M\) (\(M\) in the \(do\) operator). We do not simply statistically condition on \(M\) because it may open up some back-door path where \(M\) is a collider.

3. Natural Direct Effect:

   $$NDE = E[f_Y(x_2, f_M(x_1, U_M), U_Y)] - E[f_Y(x_1, f_M(x_1, U_M), U_Y)]$$ $$NDE = E[Y_{x_2, M_{x_1}}] - E[Y_{x_1, M_{x_1}}]$$

   \(NDE\) measures the expected change in the outcome \(Y\) when \(X\) changes \(X=x_1\) to \(X=x_2\), while \(M\) is set to the value it would have obtained before \(X\) changes, i.e., under \(X=x_1\). The second line simply introduces the notations assigned to the quantities in the first line for brevity.

4. Natural Indirect Effect:

   $$NIE = E[f_Y(x_1, f_M(x_2, U_M), U_Y)] - E[f_Y(x_1, f_M(x_1, U_M), U_Y)] $$ $$NIE = E[Y_{x_1, M_{x_2}}] - E[Y_{x_1, M_{x_1}}]$$

\(NIE\) measures the expected change in the outcome \(Y\) when \(X\) is held constant at \(X=x_1\), and \(M\) is set to the value it would have obtained in case \(X\) changes from \(x_1\) to \(x_2\).

4.2.1. Intuition

\(≫ CDE\) would take different values corresponding the level of \(M\) is set to. \(CDE\) answers the question "How would \(X\) affect \(Y\) when \(M\) was held fixed at \(m\)?".

\(≫ NDE\) addresses the concern "Suppose \(M\) did not respond to changes in \(X\), how would the effect be?" You can think of this case as \(CDE\) where \(m\) is chosen to be the value it takes before the change. However, it is called natural because \(NDE\) measures the effect transmitted to \(Y\) by preventing \(M\) from responding to changes in \(X\) i.e., disabling the indirect causal path.

\(≫ NIE\) examines a scenario where in reality we do not intervene on \(X\), but magically know the values \(M\) would take had the change to \(X\) been in place. \(NIE\) quantifies the portion of effect explained by \(M\) by disabling the direct causal effect.

I further introduce the Reverse Natural Indirect Effect \(NIE_r\), constructing by exchanging \(x_1\) with \(x_2\) $$NIE_r = E[f_Y(x_2, f_M(x_1, U_M), U_Y)] - E[f_Y(x_2, f_M(x_2, U_M), U_Y)] $$ $$NIE_r = E[Y_{x_2, M_{x_1}}] - E[Y_{x_2, M_{x_2}}]$$

You should notice that the would have notions of natural effects give rise to the counterfactual terms where the input \(X\) value to compute \(M\) is different from the value \(X\) is set to. When they are equal, which is equivalent to allowing the causal effect to pass through to \(M\), we end up with the interventional distribution. Hence, $$E[Y_{x_2, M_{x_2}}] = E[Y|do(X=x_2)], E[Y_{x_1, M_{x_1}}] = E[Y|do(X=x_1)]$$ A careful observation gives us (try proving this yourself) $$TE = NDE - NIE_r$$

4.2.2. Identifying Natural Effects

This section presents sufficient conditions for identifying the natural direct effects and the natural indirect effects. The knowledge is gratefully extracted from the paper Interpretation and Identification of Causal Mediation (Pearl 2014). The notion of identifiability is similar to what is applied to causal (interventional) quantities: we seek to reduce the counterfactual probabilities to observational or interventional ones to be estimated with techniques provided in Chapter 2.

The key condition that renders this practice possible is unconfoundeness.

Definition of Unconfoundeness and Deconfounder:

\(X\) and \(Y\) are said to be unconfounded if the variables influencing \(X\) are independent of those influencing \(Y\) when \(X\) is held fixed. A covariate or set of variates \(W\) is said to deconfound the relationship between \(X\) and \(Y\) if conditioning \(W\) blocks all back-door paths between them.

Let's revisit Figure 1.2* where \(Z\) is a common cause of \(X\) and \(Y\) and it is called a confounder. Note again that \(Z\) can be a set of common causes.



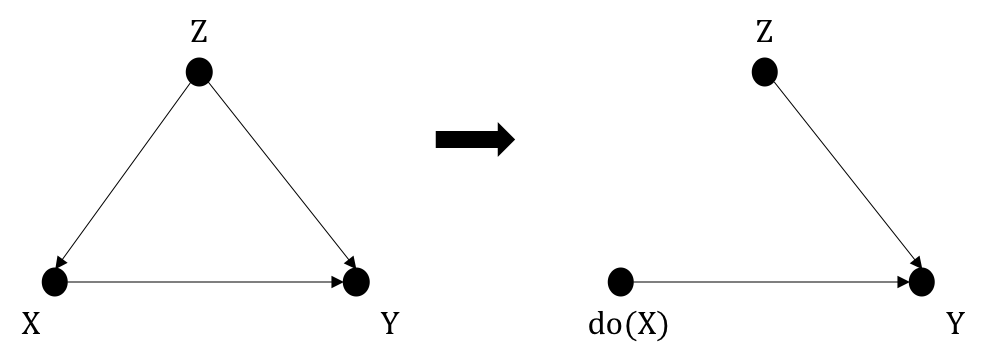
In this example, \(Z\) is also called a deconfounder because conditioning on \(Z\) blocks the back-door path that produces spurious correlations between \(X\) and \(Y\). In Figure 4.1, the \(M \rightarrow Y\) relationship is confounded both through \(X\) and through latent factors underlying the dashed path between \(U_M\) and \(U_Y\). \(X\) here is a confounder, but not a deconfounder since conditioning on \(X\) is not sufficient to block all back-door paths. The set \(W = \{X, U_M\}\) or \(W = \{X, U_Y\}\) would do the work, however, only if either \(U_M\) or \(U_Y\) is measurable.

Recall that the setting for a causal mediation problem is described in Figure 4.1. There are two main sets of conditions, \(A\) and \(B\), that are sufficient for identifying both natural effects. Each set is accompanied by its own formula.

Assumption set \(A\):

There exists a set of measure covariates \(W\) such that


1. No member of \(W\) is a descendent of \(X\)


2. \(W\) blocks all back-door paths from \(M\) to \(Y\) not going through \(X\). Holding \(X\) constant, \(W\) deconfounds the \(M \rightarrow Y\) relationship


3. \(P(m|do(t),w)\): the \(W\)-specific effect of \(X\) on \(M\) is identifiable


4. \(P(y|do(t,m),w)\): the \(W\)-specific joint effect of \(\{X,M\}\) on \(Y\) is identifiable

When conditions \(A1\) and \(A2\) hold, the natural effects are identified as

\(≫ (1a) \ NDE = \sum_m \sum_w [E(Y|do(X=x_2, M=m), W=w) - E(Y|do(X=x_1, M=m), W=w)] \) $$ P(M=m|do(X=x_1),W=w)P(W=w) $$

\(≫ (1b) \ NIE = \sum_m \sum_w E(Y|do(X=x_1, M=m), W=w) \) $$[P(M=m|do(X=x_2), W=w) - P(M=m|do(X=x_1), W=w)]P(W=w)$$

When conditions \(A1\) through \(A4\) hold, the \(do-\)expressions are reduced to observational quantities. Equations \((1a), (1b)\) become

\(≫ (2a) \ NDE = \sum_m \sum_w [E(Y|X=x_2, M=m, W=w) - E(Y|X=x_1, M=m, W=w)] \) $$ P(M=m|X=x_1,W=w)P(W=w) $$

\(≫ (2b) \ NIE = \sum_m \sum_w E(Y|X=x_1, M=m, W=w) \) $$[P(M=m|X=x_2, W=w) - P(M=m|X=x_1, W=w)]P(W=w)$$

Without \(A3\) and \(A4\), we would have to conduct randomized experiments to substantiate the interventional probabilities.

If \(A1\) and \(A2\) hold with an empty set \(W = \{\emptyset\}\) and two other sets \(W_2, W_3\) exist such that

• \(W_2\) deconfounds the \(X \rightarrow M\) relationship
• \(W_3\) deconfounds the \(\{X,M\} \rightarrow Y\) relationship

Regardless any dependencies between \(W_2\) and \(W_3\), the natural effects are given as

\(≫ (3a) \ NDE = \sum_m \sum_{w_3} [E(Y|X=x_2, M=m, W_3=w_3) - E(Y|X=x_1, M=m, W_3=w_3)] \) $$ P(W_3=w_3) \sum_{w_2} P(M=m|X=x_1,W_2=w_2)P(W_2=w_2) $$

\(≫ (3b) \ NIE = \sum_m \sum_{w_3} E(Y|X=x_1, M=m, W_3=w_3)P(W_3=w_3) \) $$\sum_{w_2}[P(M=m|X=x_2, W_2=w_2) - P(M=m|X=x_1, W_2=w_2)]P(W_2=w_2)$$

Assumption set \(B\):

There exists a set of measure covariates \(W\) such that


1. No member of \(W\) is a descendent of \(X\)


2. \(W\) and \(X\) blocks all back-door paths from \(M\) to \(Y\). Holding \(X\) constant, \(\{W,X\}\) deconfounds the \(M \rightarrow Y\) relationship


3. \(W\) blocks all back-door paths from \(X\) to \(M\) or to \(Y\)

Under condition set \(B\), the natural effects are identified through equations \((2a)\) and \((2b)\).

4.3. Case Study: Simpson's Paradox in COVID 19

Simpson's Paradox was once a tough puzzle to statisticians until Causal Infernece came in explaining it nicely with a simple causal graph. The paradox has recently made its appearance in an analysis of COVID-19 case fatility rates (CFRs) across different countries. The dataset consists of \(756,004\) confirmed Covid-19 cases and \(68,508\) fatalities reported from \(11\) different countries and segregated into age groups of \(10\)-year intervals.



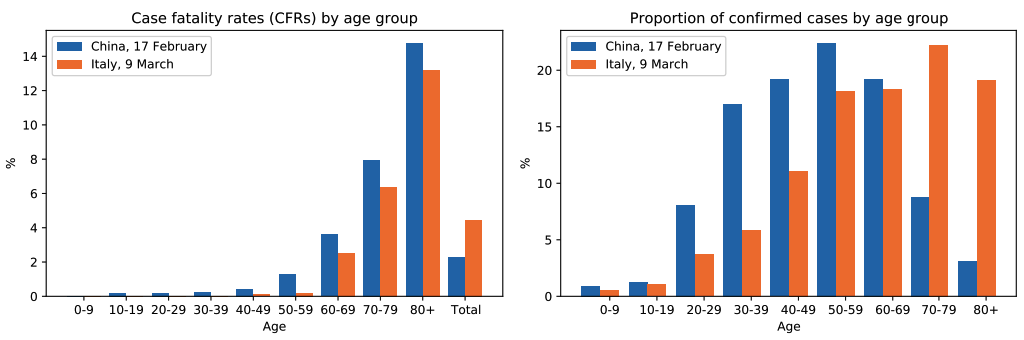
An classic paradoxical pattern is observed: for all age groups, CFRs in Italy are lower than those in China, but the total CFR in Italy is higher than that in China.

Considering the causal graph below, in which Age \(A\) is viewed as a mediator on the causal path from country \(C\) to case fatility \(F\).



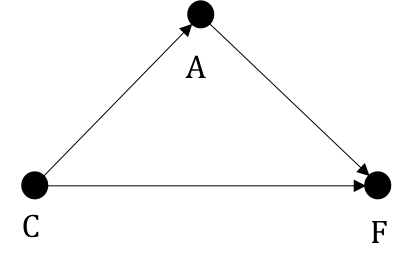
Let's define our causal mechanism more rigorously

• \(C\) : a categorical variable for the country for which CFRs are reported
• \(A\) : an ordinal variable for \(10\)-year-interval age groups of positively tested patients
• \(F\) : a binary variable for whether a patient has died \((F = 1)\) or not \((F = 0)\)
• \(C \rightarrow A\) reflects difference in age demographics between countries
• \(A \rightarrow F\) captures the fact that elderly people have higher risk of contracting the virus
• \(C \rightarrow F\) refers to country-specific effects on case fatility other than age, such as medical infrastructure, air pollution levels, and other non-pharmaceutical interventions and policies.

Figure 4.3 illustrates a familar setting for Mediation Analysis. Separating the data by age groups is equivalent to conditioning on \(A\), which blocks the indirect causal path \(C \rightarrow A \rightarrow F\). Thus, the age-specific CFRs only explains the direct effect of \(C\) on \(F\). On the other hand, the total rate takes both effects into account, and the effect of \(C\) on \(F\) is influenced by the effect from \(A\). The authors hypothesizes that CFRs is higher in Italy in total because the population is Italy is older on average than China, thus more likely to die from the disease. In fact, Figure 4.2 shows that most of the confirmed cases in Itality were reported in people aged \(60+\) while the range of China was between \(30\) and \(59\), for whom the virus is less dangerous.

While the need for cross-country comparison remains, Mediation Analysis comes in handy to disentangle direct and indirect effects. The causal difference between two countries is equivalent to the causal effects from Here the authors assume no unobserved confounders and \(C\) sufficiently deconfounds the \(A \rightarrow F\) relationship. All causal effects are thus identifable through conditional probabilities, and equations \((2a)\) and \((2b)\) are applied to measure the natural effects.

Direct and Indirect Effects on Case Fatility

1. Total Effect

What would be the effect on fatality of changing country from China to Italy? $$TE = E(F|do(C=Italy)) - E(F|do(C=China)) = E(F|C=Italy) - E(F|C=China) $$

2. Controlled Direct Effect

What would be the effect on fatality if Chinese \(50-59\)-year-olds were to live in Italy?

Recall that \(CDE\) is measured at a specific level \(A=a\) of the mediator.

$$CDE = E(F|do(C=Italy, A=a))-E(F|do(C=China, A=a))$$ $$= E(F|C=Italy, A=a)-E(F|C=China, A=a)$$

3. Natural Direct Effect

What would be the effect on fatality of changing country from China to Italy but retaining the age distribution of Chinese population?

An eaiser way is to eliminate all terms containing \(w\) in equation \((2a)\).

$$NDE = \sum_a [ E(F|C=Italy, A=a) - E(F|C=China, A=a) ] P(A=a|C=China)$$

4. Natural Indirect Effect

What would be the effect on fatality in China if the age demographics had instead been that of Italy, holding everything else unchanged? $$NIE = \sum_a E(Y|C=China, A=a)[ P(Age=a|C=Italy) - P(Age=a|C=China) ]$$

Intepreting Mediation Analysis

Figure 4.4 compares \(TE\), \(NDE\) and \(NIE\) over time.



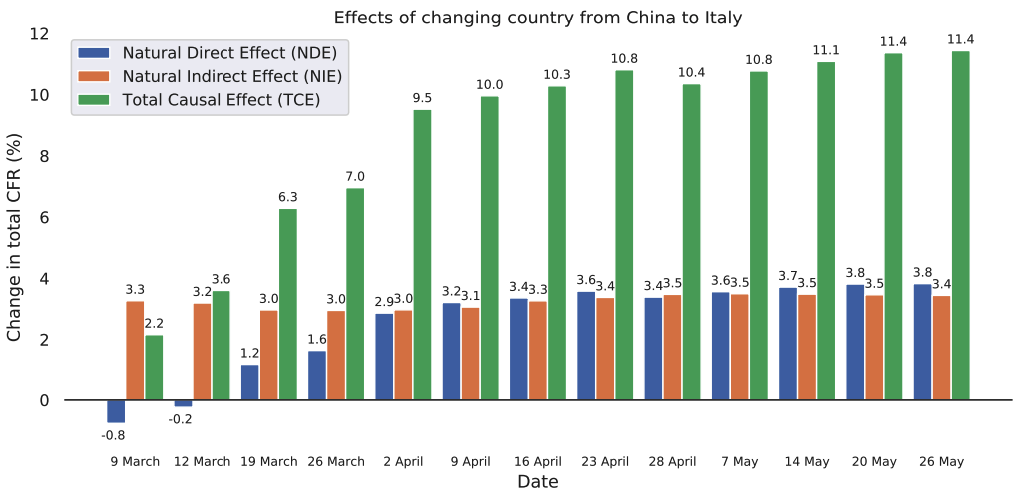
With the Chinese age demographics, it would be beneficial at first for Italy with negative \(NDE\) at the time of reporting (9 March). It is the decrease in CFRs that leads to the Italian number being lower than those of China in specific age groups. However, \(NIE\) remains high since COVID-19 would have more severe impact on China if its population was older, resulting in the higher total aggregated CFRs.

The situation gets worse as both \(NDE\) and \(NIE\) goes up over time. This signifies other country-specific factors have come into play, possibly overwhelmed heathcare system in Italy. In such a scenario, even the younger population would also be susceptible to the disease. In reality, the country did collapse under the pandemic during this time due to both old population and fragile medical infrastructure, as reflected in \(TE\) with fatility rates continue to sky-rocket.